„Assoziativgesetz“ – Versionsunterschied

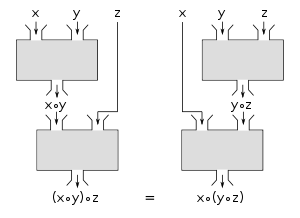
Das Assoziativgesetz (lateinisch associare „vereinigen, verbinden, verknüpfen, vernetzen“), auf Deutsch Verknüpfungsgesetz oder auch Verbindungsgesetz, ist eine Regel aus der Mathematik. Eine (zweistellige) Verknüpfung ist assoziativ, wenn die Reihenfolge der Ausführung keine Rolle spielt. Anders gesagt: Die Klammerung mehrerer assoziativer Verknüpfungen ist beliebig. Deshalb kann man es anschaulich auch „Klammergesetz“ nennen.

Neben dem Assoziativgesetz sind Kommutativgesetz und Distributivgesetz von elementarer Bedeutung in der Algebra.

Eine binäre Verknüpfung ${\displaystyle {\star }\colon A\times A\to A}$ auf einer Menge ${\displaystyle A}$ heißt assoziativ, wenn für alle ${\displaystyle a,b,c\in A}$ das Assoziativgesetz

${\displaystyle a\star \left(b\star c\right)=\left(a\star b\right)\star c}$

gilt. Die Klammern können dann weggelassen werden. Das gilt auch für mehr als drei Operanden.

Als Verknüpfungen auf den reellen Zahlen sind Addition und Multiplikation assoziativ. So gilt zum Beispiel

${\displaystyle (2+3)+7=5+7=12\quad =}$

${\displaystyle 2+(3+7)=2+10=12}$

und

Reelle Subtraktion und Division sind hingegen nicht assoziativ, denn es ist

${\displaystyle 2-(3-1)=0\quad \neq }$

${\displaystyle (2-3)-1=-2}$

und

${\displaystyle (4:2):2=1\quad \neq }$

${\displaystyle 4:(2:2)=4}$ .

Auch die Potenz ist nicht assoziativ, da

${\displaystyle 2^{(2^{3})}=2^{8}=256\quad \neq }$

${\displaystyle (2^{2})^{3}=4^{3}=64}$

gilt. Bei (divergenten) unendlichen Summen kann es auf die Klammersetzung ankommen. So verliert die Addition die Assoziativität bei:

${\displaystyle (1+(-1))+(1+(-1))+(1+(-1))+(1+(-1))+\ldots =0+0+\ldots \to 0}$

aber

${\displaystyle 1+((-1)+1)+((-1)+1)+((-1)+1)+\ldots =1+0+0+\ldots \to 1}$

Das Assoziativgesetz gehört zu den Gruppenaxiomen, wird aber bereits für die schwächere Struktur einer Halbgruppe gefordert.

Insbesondere bei nicht-assoziativen Verknüpfungen gibt es Konventionen einer seitigen Assoziativität.

Eine binäre Verknüpfung ${\displaystyle *}$ gilt als links-assoziativ, wenn

${\displaystyle {\begin{array}{ll}a*b*c&:=(a*b)*c\qquad \qquad \quad \,\\a*b*c*d&:=((a*b)*c)*d\quad \\{\mbox{etc.}}\end{array}}}$

aufzufassen ist.

• Die nicht-assoziativen Operationen Subtraktion und Division werden gemeinhin links-assoziativ verstanden:^[1][2][3]

	${\displaystyle a-b-c}$	${\displaystyle =(a-b)-c}$	(Subtraktion)
	${\displaystyle a:b:c}$	${\displaystyle =(a:b):c}$	(Division)

• Anwendung von Funktionen
  ${\displaystyle (f\,x\,y)=((f\,x)\,y)}$
  im Verfahren des Currying.

Eine binäre Verknüpfung ${\displaystyle *}$ heißt rechts-assoziativ, wenn gilt:

${\displaystyle {\begin{array}{rr}x*y*z:=&x*(y*z)\\w*x*y*z:=&w*(x*(y*z))\\&{\mbox{etc.}}\end{array}}}$

Beispiel für eine rechts-assoziative Operation:

• Exponenzieren reeller Zahlen in Exponentenschreibweise:

${\displaystyle x^{y^{z}}=x^{(y^{z})}}$

Aber auch assoziative Operationen können Seitigkeit haben, wenn sie ins Unendliche zu iterieren sind.

• Die dezimale Notation rechts vom Dezimalkomma
  ${\displaystyle 0{,}999\ldots =0{,}9999\ldots =0{,}99999\ldots \to 1}$
  ist eine links-assoziative Verkettung der Dezimalziffern, weil die Auswertung(sschleife) nicht rechts bei den Auslassungspunkten ${\displaystyle \ldots }$ beginnen kann, sondern links beginnen muss.
• Die ${\displaystyle p}$-adische Schreibweise
  ${\displaystyle \ldots 444_{5}=\ldots 4444_{5}=\ldots 44444_{5}\to -1}$
  enthält mit der Juxtaposition eine rechts-assoziative Verkettungsoperation, weil die Auswertung rechts beginnen muss.

Folgende Abschwächungen des Assoziativgesetzes werden an anderer Stelle genannt/definiert:

• Potenz-Assoziativität:
  ${\displaystyle a^{r+s}=(a^{r})\circ (a^{s})}$
  • i-Potenz-Assoziativität:
    ${\displaystyle a^{i}\circ a=a\circ a^{i}}$
  • Idemassoziativität:
    ${\displaystyle a\circ (a\circ a)=(a\circ a)\circ a}$
• Alternativität:
  • Linksalternativität:
    ${\displaystyle a\circ (a\circ b)=(a\circ a)\circ b}$
  • Rechtsalternativität:
    ${\displaystyle a\circ (b\circ b)=(a\circ b)\circ b}$
• Flexibilitätsgesetz:
  ${\displaystyle a\circ \left(b\circ a\right)=\left(a\circ b\right)\circ a}$
• Moufang-Identitäten:
  ${\displaystyle {\Big (}a\circ (b\circ a){\Big )}\circ c=a\circ {\Big (}b\circ (a\circ c){\Big )}}$
  ${\displaystyle (a\circ b)\circ (c\circ a)=a\circ {\Big (}(b\circ c)\circ a{\Big )}}$
• Bol-Identitäten:^[4]
  • linke Bol-Identität:
    ${\displaystyle {\Big (}b\circ (c\circ b){\Big )}\circ a=b\circ {\Big (}c\circ (b\circ a){\Big )}}$
  • rechte Bol-Identität:
    ${\displaystyle {\Big (}(a\circ b)\circ c{\Big )}\circ b=a\circ {\Big (}(b\circ c)\circ b{\Big )}}$
• Jordan-Identität:
  ${\displaystyle a\circ {\Big (}\left(a\circ a\right)\circ b{\Big )}=\left(a\circ a\right)\circ \left(a\circ b\right)}$

• Algebra
• Operatorassoziativität

• Otto Forster: Analysis 1: Differential- und Integralrechnung einer Veränderlichen. Vieweg-Verlag, München 2008, ISBN 978-3-8348-0395-5. 

1. ↑ Bronstein: Taschenbuch der Mathematik. Kapitel: 2.4.1.1, ISBN 978-3-8085-5673-3, S. 115–120
2. ↑ George Mark Bergman: Order of arithmetic operations
3. ↑ The Order of Operations. Education Place
4. ↑ Gerrit Bol: Gewebe und Gruppen In: Mathematische Annalen, 114 (1), 1937, S. 414–431.